Divisibilidad por 13
Un número es divisible por 13 si multiplicando las unidades por 1, las decenas por -3, las centenas por -4, las unidades de millar por -1, las decenas de millar por 3, las centenas de millar por 4 y así sucesivamente, alternando los signos, y sumando los resultados el número resultante es divisible por 13
Vamos a demostrar el criterio de divisibilidad por 13.
(an10n + an-110n-1 + ...+ a110 + a0) mod 13 =
an10n mod 13 + an-110n-1 mod 13 + ...+ a110 mod 13 + a0 mod 13 =
an mod 13 10n mod 13 + an-1 mod 13 10n-1 mod 13 + ...+ a1 mod 13 10 mod 13 + a0 mod 13
100 mod 13 = 1
101 mod 13 = -3
102 mod 13 = -4
103 mod 13 = -1
104 mod 13 = 3
105 mod 13 = 4
Así, supongamos el número: 6874259642754. Según la teoría de las clases residuales mod 7 con sus operaciones, tendríamos que multiplicar la cifra de las unidades por 1, la de las decenas por 3, la de las centenas por 2, la de las unidades de mil por 6 (o por –1), la de las decenas de mil por 4 (o por –3), la de las centenas de mil, por 5 (o por –2), y así sucesivamente.
¿No resultaría práctico disponer el número dividido en grupos de tres cifras y considerar alternativamente positivas las cifras del primero, negativas las del segundo, positivas las del tercero, etc. Y así multiplicaríamos:
La suma algebraica de las unidades de cada grupo, por 1,
La suma algebraica de las decenas de cada grupo, por -3,
y la suma algebraica de las centenas de cada grupo, por -4? Esta suma módulo 13 sería el resto.
Losa restos potenciales de 13 son 1, -3, -4, -1, 3, 4, 1, -3, -4, -1, 3, 4 etc. Haciendo algo análogo tendríamos:
+6 ; - 874 ; + 259 ; - 642 ; + 754
4 – 2 + 9 – 4 + 6 = 13 que mod 13 sería 0 0 · 1 = 0
5 – 4 + 5 – 7 = -1 que mod 13 sería -1 -1 · (-3) = 3
7 – 6 + 2 – 8 = -5 que mod 13 sería -5 · (-4) = 20. Suma 23 mod 13 = 10 por lo que no es divisible por 13.
Esta es la razón por la que un número cualquiera de tres cifras como 649 ampliado por repetición de las mismas cifras 649649, siempre será divisible por 7, 11, y 13.
Lo mismo que un número de cuatro cifras 7538 ampliado por repetición de las mismas cifras, 75385387, siempre será divisible por 73 y por 137. Basta ver los restos potenciales de
73 (1, 10, 27,-22, -1, -10, -27, 22, …. ) y 137 (1, 10, -37, 41, -1, -10, 37, -41, ….)
martes, 12 de mayo de 2009
Teoria de Conjuntos
INTRODUCCIÓN A LA TEORÍA DE CONJUNTOS
Rama de las matemáticas a las que el matemático Georg Ferdinand Ludwing Philipp Cantor es el padre de la Teoría de Conjuntos, dio su primer tratamiento formal en 1870. El concepto de conjunto es uno de los más fundamentales en matemáticas, incluso más que la operación de contar, pues se puede encontrar implícita o explícitamente, en todas las ramas de las matemáticas puras y aplicadas. En su forma explícita, los principios y terminología de los conjuntos se utilizan para construir proposiciones matemáticas más claras y precisas y para explicar conceptos abstractos como el infinito. En el año 1874, apareció el primer trabajo revolucionario de Cantor sobre la Teoría de conjuntos.
DEFINICIONES
Sabemos que la palabra conjunto implica la idea de una colección de objetos que se caracterizan en algo común. En matemática tiene el mismo significado, sólo que a estos objetos se les llama elementos o miembros del conjunto. La noción simple de una colección o conjunto de objetos es fundamental en la estructura básica de las matemáticas y fue Georg Cantor, en los años 1870 quien primero llamó la atención de los matemáticos a este respecto. No puede darse una definición satisfactoria de un conjunto en términos de conceptos simples, por lo tanto la palabra "CONJUNTO" debe aceptarse lógicamente como un término no definido.
Un conjunto es una colección bien definida de objetos de cualquier clase.
DETERMINACIÓN DE UN CONJUNTO
Hay dos formas de determinar conjuntos.
Ejemplos.
A = { a, e, i, o, u }
B = { 0, 2, 4, 6, 8 }
C = { c ,o ,n , j, u, t, s } En un conjunto determinado por extensión no se repite un mismo elemento.
Ejemplos.
A = {x/x es una vocal}
B = {x/x es un número par menor que 10}
C = {x/x es una letra de la palabra conjuntos}
Vamos a mostrarte un cuadro comparativo de determinación de conjuntos
A = { a, e, i, o, u } A = { x/x es una vocal }
B = { 0, 2, 4, 6, 8 } B = { x/x es un número par menor que 10 }
C = { c, o , n, j, u, t, s } C = { x/x es una letra de la palabra conjuntos }
D = { 1, 3, 5, 7, 9 } D = { x/x es un número impar menor que 10 }
E = { b, c, d, f, g, h, j, . . . } E = { x/x es una consonante }
CONJUNTOS FINITOS
Un conjunto es finito si consta de un cierto número de elementos distintos, es decir si al contar los diferentes elementos del conjunto el proceso de contar puede acabar. En caso contrario, el conjunto es infinito.
M = { x / x es un río de la tierra } Conjunto finito
N = { 0, 1, 2, 3, 4, 5, 6, 7, 8, ... } Conjunto infinito
P = { x / x es un país de la tierra } Conjunto finito
V = { 3, 6, 9, 12, 15, 18, 21, 24, 27, ... } Conjunto infinito
IGUALDAD DE CONJUNTOS
Se dice que 2 conjuntos A y B son iguales cuando ambos tienen los mismos elementos, es decir si cada elemento de A pertenece a B y si cada elemento que pertenece a B pertenece también A La igualdad se denota A = B.
A = {1, 2, 3, 4}
B = {3, 4, 1, 2}
A = B
C = {1, 2, 3, 3, 4, 1}
D = {1, 2, 2, 3, 4, 4,}
C = D
E = {vocal de la palabra mundo}
F = {u, o}
E = F
DIAGRAMA DE VENN
A cada conjunto se le considera encerrado dentro de una curva (plana) cerrada. Los elementos del conjunto considerado pueden ser específicamente dibujados o pueden quedar (implícitamente) sobreentendidos. Los diagramas son empleados, para representar tanto a los conjuntos como a sus operaciones, y constituyen una poderosa herramienta geométrica, desprovista de validez lógica. A continuación representaremos algunos conjuntos y verificaremos algunas igualdades (las intersecciones de dos o más conjuntos quedan caracterizados por el rayado múltiple).
El gráfico es la representación de la unión.

El gráfico es la representación de la intersección.

El gráfico es la representación de la diferencia.

En forma gráfica:
Vamos a mostrarle 3 formas graficas.
Rama de las matemáticas a las que el matemático Georg Ferdinand Ludwing Philipp Cantor es el padre de la Teoría de Conjuntos, dio su primer tratamiento formal en 1870. El concepto de conjunto es uno de los más fundamentales en matemáticas, incluso más que la operación de contar, pues se puede encontrar implícita o explícitamente, en todas las ramas de las matemáticas puras y aplicadas. En su forma explícita, los principios y terminología de los conjuntos se utilizan para construir proposiciones matemáticas más claras y precisas y para explicar conceptos abstractos como el infinito. En el año 1874, apareció el primer trabajo revolucionario de Cantor sobre la Teoría de conjuntos.
DEFINICIONES
Sabemos que la palabra conjunto implica la idea de una colección de objetos que se caracterizan en algo común. En matemática tiene el mismo significado, sólo que a estos objetos se les llama elementos o miembros del conjunto. La noción simple de una colección o conjunto de objetos es fundamental en la estructura básica de las matemáticas y fue Georg Cantor, en los años 1870 quien primero llamó la atención de los matemáticos a este respecto. No puede darse una definición satisfactoria de un conjunto en términos de conceptos simples, por lo tanto la palabra "CONJUNTO" debe aceptarse lógicamente como un término no definido.
Un conjunto es una colección bien definida de objetos de cualquier clase.
DETERMINACIÓN DE UN CONJUNTO
Hay dos formas de determinar conjuntos.
- Por extensión ó Forma tabular.
Se dice que un conjunto es determinado por extensión (o enumeración), cuando se da una lista que comprende a todos los elementos del conjunto y sólo a ellos.
Ejemplos.
A = { a, e, i, o, u }
B = { 0, 2, 4, 6, 8 }
C = { c ,o ,n , j, u, t, s } En un conjunto determinado por extensión no se repite un mismo elemento.
- Por comprensión ó Forma Constructiva
Se dice que un conjunto es determinado por comprensión, cuando se da una propiedad que la cumpla en todos los elementos del conjunto y sólo a ellos.
Ejemplos.
A = {x/x es una vocal}
B = {x/x es un número par menor que 10}
C = {x/x es una letra de la palabra conjuntos}
Vamos a mostrarte un cuadro comparativo de determinación de conjuntos
A = { a, e, i, o, u } A = { x/x es una vocal }
B = { 0, 2, 4, 6, 8 } B = { x/x es un número par menor que 10 }
C = { c, o , n, j, u, t, s } C = { x/x es una letra de la palabra conjuntos }
D = { 1, 3, 5, 7, 9 } D = { x/x es un número impar menor que 10 }
E = { b, c, d, f, g, h, j, . . . } E = { x/x es una consonante }
CONJUNTOS FINITOS
Un conjunto es finito si consta de un cierto número de elementos distintos, es decir si al contar los diferentes elementos del conjunto el proceso de contar puede acabar. En caso contrario, el conjunto es infinito.
M = { x / x es un río de la tierra } Conjunto finito
N = { 0, 1, 2, 3, 4, 5, 6, 7, 8, ... } Conjunto infinito
P = { x / x es un país de la tierra } Conjunto finito
V = { 3, 6, 9, 12, 15, 18, 21, 24, 27, ... } Conjunto infinito
IGUALDAD DE CONJUNTOS
Se dice que 2 conjuntos A y B son iguales cuando ambos tienen los mismos elementos, es decir si cada elemento de A pertenece a B y si cada elemento que pertenece a B pertenece también A La igualdad se denota A = B.
A = {1, 2, 3, 4}
B = {3, 4, 1, 2}
A = B
C = {1, 2, 3, 3, 4, 1}
D = {1, 2, 2, 3, 4, 4,}
C = D
E = {vocal de la palabra mundo}
F = {u, o}
E = F
DIAGRAMA DE VENN
A cada conjunto se le considera encerrado dentro de una curva (plana) cerrada. Los elementos del conjunto considerado pueden ser específicamente dibujados o pueden quedar (implícitamente) sobreentendidos. Los diagramas son empleados, para representar tanto a los conjuntos como a sus operaciones, y constituyen una poderosa herramienta geométrica, desprovista de validez lógica. A continuación representaremos algunos conjuntos y verificaremos algunas igualdades (las intersecciones de dos o más conjuntos quedan caracterizados por el rayado múltiple).
El gráfico es la representación de la unión.

El gráfico es la representación de la intersección.

El gráfico es la representación de la diferencia.

UNIÓN DE CONJUNTOS
La unión de los conjuntos A y B es el conjunto formado por todos los elementos que pertenecen a A o a B o a ambos. Se denota: A U B. La unión de conjuntos se define como:
A U B = {x / x A o x B}
En forma gráfica:
Vamos a mostrarle 3 formas graficas.
Ejemplos:
1. Dados los conjuntos: A = { 0, 1, 2, 3, 4, 5 }, B = { 0, 2, 4 } y C = { 5, 6, 8 }, efectuar y construir los diagramas respectivos:
a) A U C b) B U C c) A U B
Tenemos que Observar el siguiente ejemplo.
a) A = { 0, 1, 2, 3, 4, 5 } y C = { 5, 6, 8 }


A U C = { 0, 1, 2, 3, 4, 5, 6, 8 }
Representación gráfica de la unión de conjuntos A y C
b) B = { 0, 2, 4 } y C = { 5, 6, 8 }
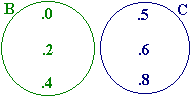

B U C = { 0, 2, 4, 5, 6, 8 }
Representación gráfica de la unión de conjuntos B y C
c) A = { 0, 1, 2, 3, 4, 5 } y B = { 0, 2, 4 }


A U B = {0, 1, 2. 3, 4, 5 }
Representación gráfica de la unión de conjuntos A y B
By: Daniel Pariente Delgadillo
Facil no ?? jajaja :)
Creo que FalTa Algo Mas..... ^^??


A U C = { 0, 1, 2, 3, 4, 5, 6, 8 }
Representación gráfica de la unión de conjuntos A y C
b) B = { 0, 2, 4 } y C = { 5, 6, 8 }


B U C = { 0, 2, 4, 5, 6, 8 }
Representación gráfica de la unión de conjuntos B y C
c) A = { 0, 1, 2, 3, 4, 5 } y B = { 0, 2, 4 }


A U B = {0, 1, 2. 3, 4, 5 }
Representación gráfica de la unión de conjuntos A y B
By: Daniel Pariente Delgadillo
Facil no ?? jajaja :)
lunes, 11 de mayo de 2009
Suscribirse a:
Entradas (Atom)



